〽️
Non-linear predictor outcome associations
勉強目標:Ho 2023 BMJ Med. を読んで、非線形性な変数とアウトカムの関係を捉えるモデル(NatureもしくはRestricted Cubic Spline)の概要を理解する。また、Rで実装できるようになること。
本日の文献(1) Ho 2023 BMJ Med

Ho 2023の解説
Introduction
FIgure1の紫の実線は、Understanding Society研究の12435人の参加者におけるBMIとMental wellbeingの関連に当てはめた直線(Assumed lenear)を表しています。
このモデルでは、BMIが1単位増加するごとに、BMIの範囲全体で精神的なウェルビーイングが0.03単位悪化することを示しています。この場合、BMIが19と20の個人と、BMIが39と40の個人の間には同じ差があるといことになりますが、これはBMIとMental wellbeingの関係を正しく表しいるとは言えません。そこで、この問題を解決する方法として以下の3つが選択肢となる。
非線形関連を示す方法
1) 連続変数をカテゴリー化する
2) 多項式回帰
3) スプライン回帰
1) 予測変数のカテゴリー化
例(Figure 1):BMI を肥満 (≥30) と非肥満 (<30) グループに分割するなどの二分化。
問題点
- 統計的検出力が失われること
- カテゴリに分けたとしてもカテゴリの中の個々の値とアウトカムは同等の関連性を持つという仮定に基づいているため。
例(Figure 1):低BMIと高BMIのグループでは、関連性がなくなってしまった(FIgure1. のピンクの破線と黄色の破線)。
より多くのグループで分類すると、非線形性に対応できる可能性もあるが、
- カットポイントは任意(arbitrary)であり、結果は依然として不正確である。


2) 多項式回帰(Modelling with explicit polynomials)
全てのデータ(例で言うとBMI)を利用して次数が 3 を超える多項式でモデリングすること。
下記の紫の実線が多項式回帰(Cubic Polynomial)。

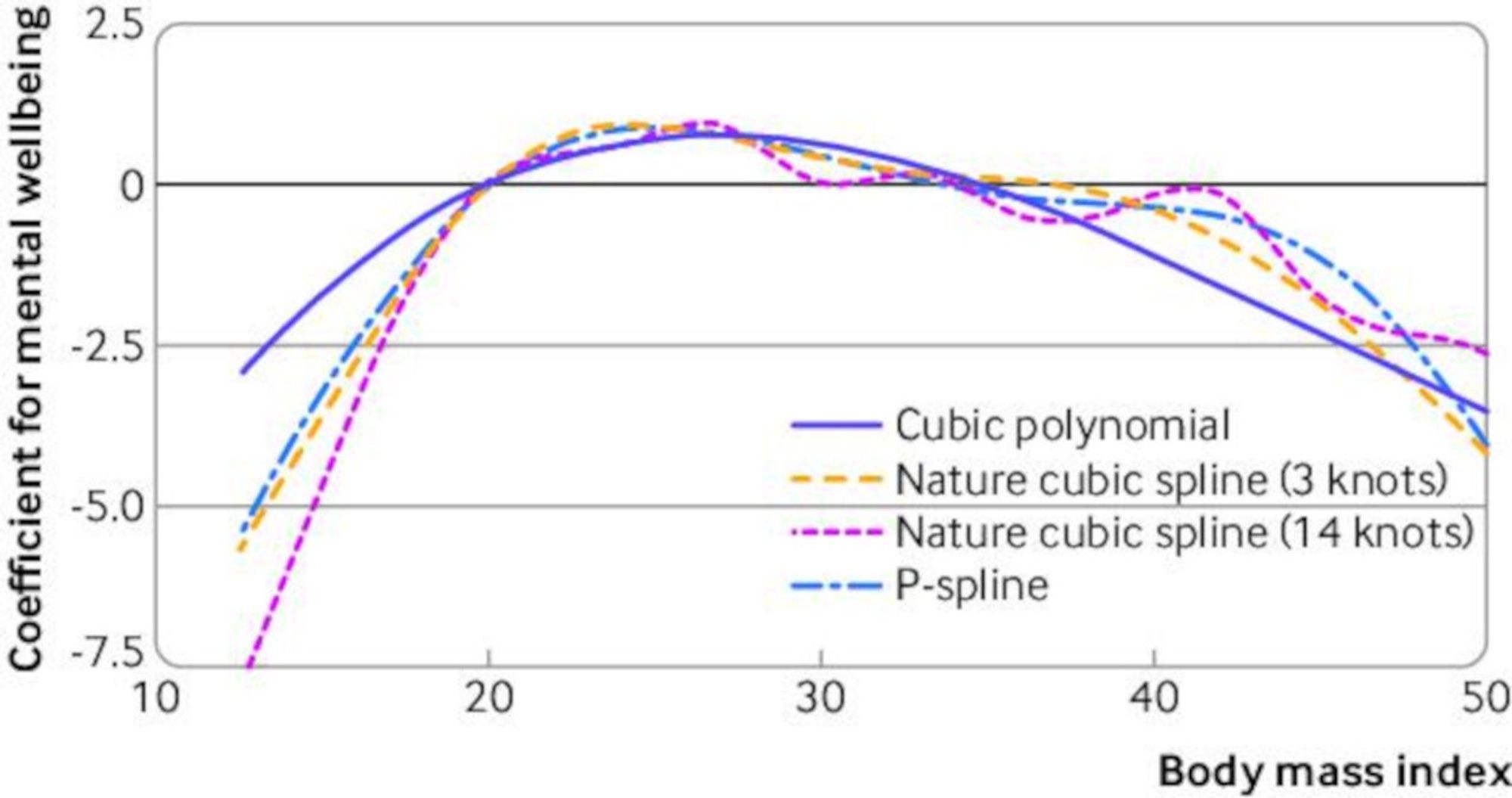
Figure 2
Association between body mass index and mental wellbeing using non-linear methods. Mental wellbeing is norm referenced with a population mean of 50 and standard deviation of 10. Adjusted for age, sex, ethnicity, education, and baseline physical and mental wellbeing. Age and wellbeing variables were adjusted as P-splines. Primary sampling units and strata were adjusted using random intercepts.
問題点
- 外れ値に敏感であること(極値にある 1 つの外れ値が曲線に顕著な影響を与える可能性がある)
- 多項式項間の相関により、推定の堅牢性が低下する可能性があること
3) スプライン回帰(Modelling with regression splines)
Figure2. の黄色とピンクの点線。Nature=Restricted。スプライン回帰は、それぞれが変数の範囲の異なるセクションに適合する一連の区分的多項式(区域毎に区切られた間の多項式の和)で構成されます。多項式が交わる場所はKnotと呼ばれます。
数式としては下記のような式
ある閾値を必ず通るようにして、ノットの変数をα1、α2、α3とおくと下記のような数式になります。

https://www.m3.com/clinical/open/news/870768 よりこれでα1、α2、α3における繋ぎ目が滑らかになるようです。
3 次スプライン回帰の長所・短所
- 各データ ポイントが、スプライン回帰で当てはめられた 3 次曲線のうち、 1 つのみに影響を与えていること(比較的)。それでも外れ値の影響をまだ受けやすい。
- 変数の両端にある多項式(境界多項式) が不安定であり、特に外れ値の影響を受けやすいことが短所。
- 上記ではOver fittingとなるため、境界曲線を直線としてモデル化し、overfittingを避けている。
- 上記をNatural(Nature) cubic splinesまたはRestricted cubic splinesと呼ぶ。
!注意点!
Natural(Nature) cubic splinesは、複雑な非線形関連を捉えることができ、外れ値に対して比較的堅牢だがKnotの数と位置に敏感です。
- 黄色の破線には 3 つのノットがあり、ピンクの破線には 14 のノットがあり、分布の分位数に配置されている。
- 回帰スプラインはノットの選択に影響されるため、アナリストはスプラインの数と配置を最適化する必要があります。
- ノットが多すぎるとオーバーフィッティングが発生し、曲線が粗くなりすぎる (図 2のピンクの線))。
- 逆に、ノットが少なすぎると、アンダーフィッティングが発生します。
- Knotsは3 ~ 5knotsが推奨される。

A data driven approach for knots
- ペナルティ付きスプライン(Penalised splines):ノット選択の影響を最小限に抑える回帰スプラインの拡張です。ラフな過適合曲線にペナルティを与えることによって行われる。
- Penalised splinesの例1:P スプライン
予測子の範囲に等間隔に配置された比較的多数のノット (多くの場合 20 以上) が含まれており、多数のノットによってアンダーフィッティングが回避されます。一方、計算上の軽い平滑化ペナルティにより、過剰適合が回避されます。Figure 2の青い破線は、適合された P スプラインを示しています。そのほか、平滑化スプライン(smoothing spline)と薄板スプライン(thin plate spline)がある(詳細は割愛)。
Modelling non-linearity in practice
- R (splines package; gam, mgcv, gamlss)
- Stata (mkspline)
- SPSS (regression procedure)
The generic term for them is generalised additive models, an extension of generalised linear models where the additive indicates non-linear fitting. These techniques can also be applied to other forms of regression, for example, logistic regression for binary data, and proportional hazards regression (Cox model) for time-to-event data. However, the non-linear link function for these regressions can affect the interpretation of linearity.
非線形性の確認(線形モデルと比較した場合の非線形性の確認)は下記で可能
- F-test
- Bayesian Information Criterion: Knotsが異なるsplines (particularly regression splines) の当てはまりを確認することができる。
スプライン回帰で結果を可視化できることは、under-fitting or over-fittinの確認の手助けになります(この場合、臨床的知識によって、Knotsの数や位置を調整可能)。
